几小时探究数学之二次函数（一）

共计 1674 个字符，预计需要花费 5 分钟才能阅读完成。

前言

咳咳，有人向我来提开一个课程，那我就开一个吧，大家 上课睡觉的（bushi）没听懂的，可以来这里看看，我会在 每一期之前 说明看这一期 所需要的相关知识（虽然有时候也可能不写就是了），有可能胡编乱造一些名词，反正你理解就是了。

路人甲：哎？不是（>_>）

管他呢，反正前言先说到这里，下面正片开始。

本期所需知识

• 一次函数基本知识
• 描点法
• 一张纸
• 一支笔
• 你的人
• 你的大脑（bushi）

我的函数基本观念

对于一个普通的一次函数：y=kx+b，通常称 k 为一次项系数 ，b 为常数项，这是一次函数的一般形式，也就是化简之后的形式，因为这样的形式可以解决许多问题，就先用下来了。

那对于其他的多次函数，类似于这样的 一般形式 存在吗？答：当然存在！

二次函数，顾名思义，也就是 x 的次数为 2 ，所以一定会出现 x²，所以，一般形式是：y=ax²+bx+c，发现了吗：这里的a 为二次项系数 ，b 为一次项系数 （和一次函数里的 k 一样），c 为常数项 （ 路人甲：我知道！和一次函数里的 b 一样！（^_^）），它就多了一个ax²。

注：这里的 a、b、c、k 都是常数（应该也不用我说明吧，写起来也怪麻烦的，后面就不写了（^_^））。

我的函数图像基本观念

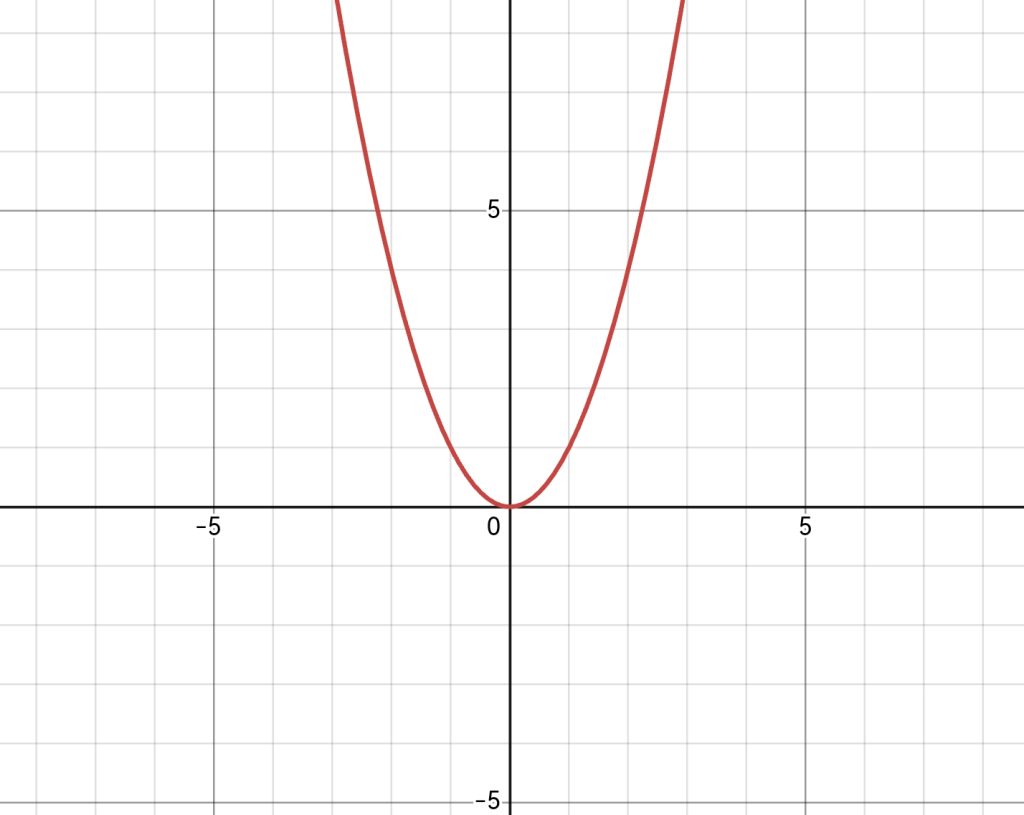
对了，本文章所有函数图像都来自Desmos，推荐去看看。

上图是二次函数的图像，对于这样一个函数图像而言，我们可以把它看作由无数个点组成，那么要画出它，就是把这些点的坐标一个一个的算出来。

路人甲：不对呀，这无数个点，不是算到天荒地老吗？

别急嘛，这么多点肯定算不完，所以就有了“采样”（我自创的名词），采样多少个点叫采样个数，我们就可以通过采样，来大致画出函数图像了，这就是所谓的“描点法 ”（这个采样点很多⊙︿⊙），所以，有了所谓的“画示意图”，也就是“ 五点法 ”，顾名思义，也就是 五个采样点，然后画出大致图像。

不过，这些等以后在详细讲解，现在，还有一个概念没有说明，那就是——偏移。

还记得我在之前一次函数 y=kx+b 中讲解的 斜率 k 和 偏移量 b 吗？

路人甲：我不到啊(◎_◎;)

回去看去！送走一位～（bushi）

咳咳，我们先讲讲 偏移量 ，也称作常数项，在二次函数中y=ax²+bx+c 中就是 c 了。究竟是什么呢？我们可以发现，当 偏移量增大 一个量，就意味着 所有点的 y 坐标 也都 增加 了这一个量，具体就是——

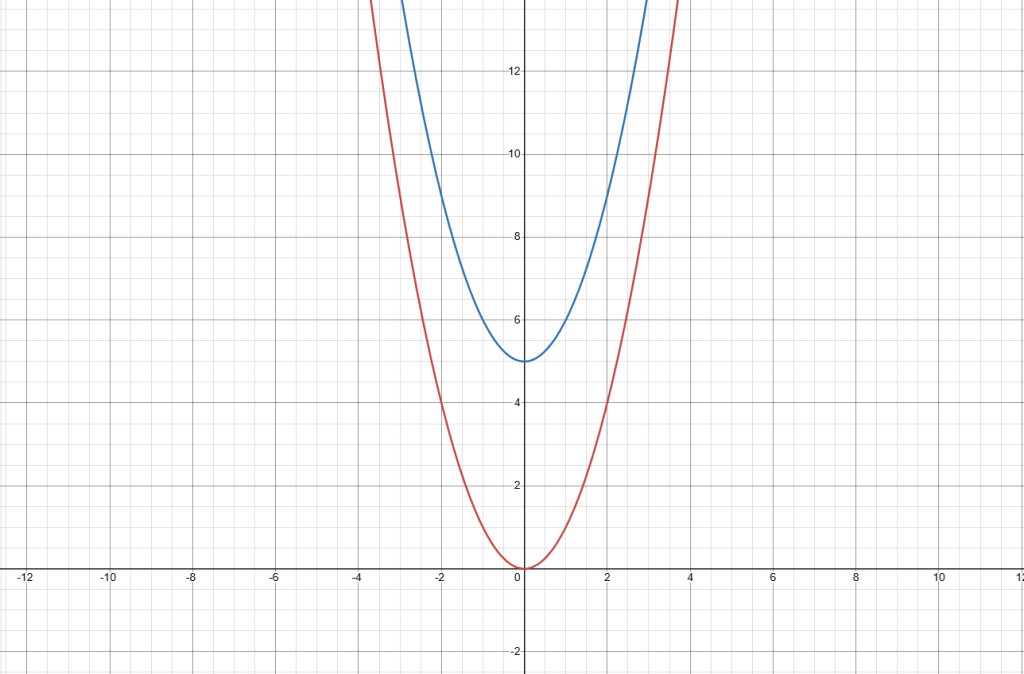
如图，两条函数图像，红色的是 y=x²，蓝色的是y=x²+5，发现不对了吗？ 每个点都向上移动 了五个单位长度，所以 整个图像向上移动 了五个单位长度！

在 一次函数 里，如 y=x 和y=x+5，就是这样的：

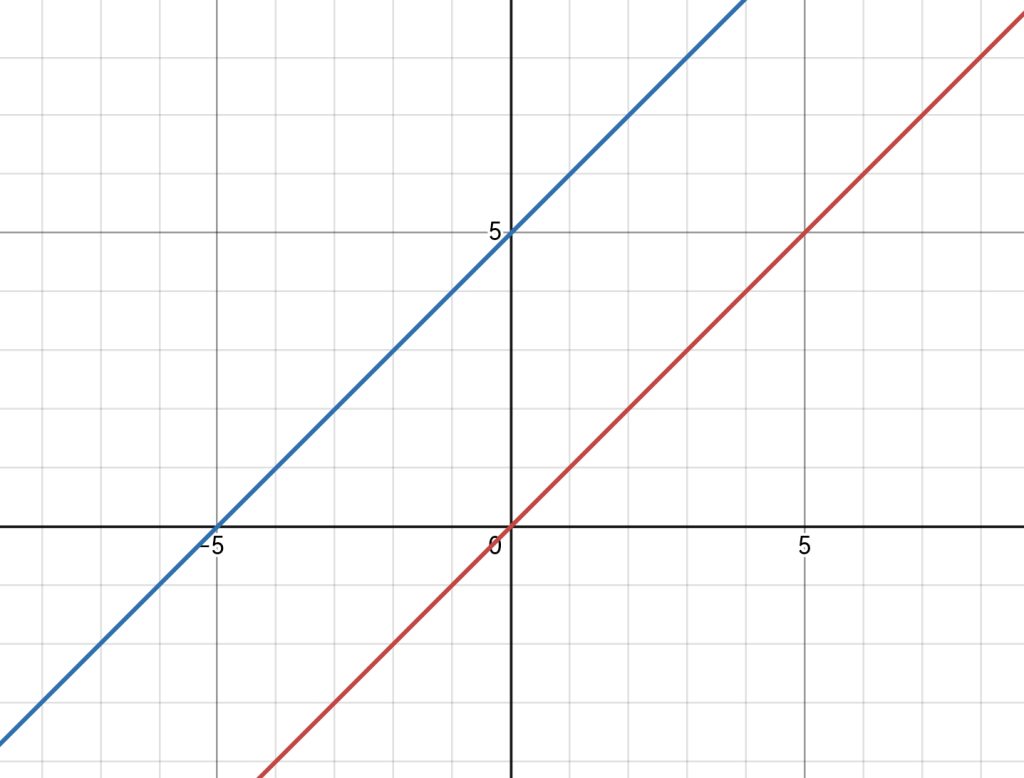
所以说，将函数图像看作无数个点的思想 是非常好用的，也是解题非常快的。

我的解题基本思想与技巧

这部分 相当简单，就仨。

路人甲：哦？(´･_･`)

是的，如下：

• 普通解法，又称正解
• 反解法，即自己想一个答案代回去看看是否与题目矛盾，适合做选择填空（莫名像反证法？（笑））
• 动态分析法 ，也就是在做动态图像题目时（讲个鬼故事： 动点 P （ಥ⌣ಥ）），实测非常的好用，无论是 最值问题 还是 变化趋势 问题，都相当的方便。

好啦，今天就先讲到这里，下次我们就要正式发车啦(#^.^#)。

番外

路人甲：呼……终于结束了，麓黎，你还没写完吗？

麓黎：刚好写完，累死我了。(´∀`)

路人甲：话说你写这个东西有什么用啊，又不给你自己看……（小声）

麓黎：你说什么？

路人甲：没什么，没什么。(´･_･`)

麓黎：你——再——说——一——遍！（莫名火大）(◣_◢)

路人甲：哎？不是不是，我……什么都没说啊，等等，你拿法杖干什么！（凝聚火球声）哎？相信我，一定要相信我！

（将法杖对准路人甲的心脏）

麓黎：再见了。ʕ•̀_•́ʔ）

（只见火球向路人甲飞去，然后……）

（砰的一声）

（倒地的声音）

麓黎 ：总算干掉啦（看着地上的 烤鸡），就是有点脏了，你清洗一下吧。

路人甲：那今天晚上就吃这个了？那碗里的是什么？我刚刚喝了一口。

麓黎：解毒剂。

路人甲：啊？？？

（ps：麓黎的火魔法会产生重金属，吃多了会重金属中毒，而副产物可以解毒）

（精神状态良好）

ʢᵕᴗᵕʡ