共计 1752 个字符,预计需要花费 5 分钟才能阅读完成。
本期所需知识
- 二元一次方程基本知识
- 配方法
二次函数基础入门
在前一章中,我们已经提到,二次函数 的基本表达式为:y=ax2+bx+c,这也被称作 一般式,因为及其的一般,平平无奇(^_^)。
那有什么方法来让它变得更 复杂 或者 好玩好看 一些呢?(精神状态良好),当然是有的!我们可以莫名的发现,当 y=0 时,这个式子就成了:ax2+bx+c=0。
路人甲 :这不是 二元一次方程 的一般式 吗?我还记得,这a≠0!
是啊,所以说,二次函数 的一般式 中, a 一定不能等于 0 。
路人甲:那等于了会发生什么呢?
会被 二向箔 一向箔 变成 一次函数。
路人甲:哦……
让我们继续研究 ax2+bx+c=0 吧,当我们要解这个方程时,可以直接:上!公!式!吗……?
而并卵,并不。秉承着玩的心情,让我们来 配方。提取a:a(x2+b/a+b2/4a2)+c-b2/4a=0
路人甲:哎?不是,发生啥了?o(~ヘ~o#)
咳咳,就只是快了一点嘛,打这个东西也是很累的嘛,就让我偷懒一下下啦。
总之,就成了:a(x+b/2a)2+(4ac-b2)/4a=0(请允许我还未掌握打分数的技能)
替换一下:a(x+b/2a)2+(4ac-b2)/4a=y!那么我们玩了个什么出来捏?不妨用一个一般式带入看看:y=2x2+4x+3 –> y=2(x+1)2+1。好熟悉啊……好像老师上课讲过?
路人甲:我不到啊,有讲吗?反正我在睡觉。(¦3[▓▓]
那么这个式子有什么意义吗?看起来好奇怪啊……让我们上,函!数!图!像!
初识函数图像
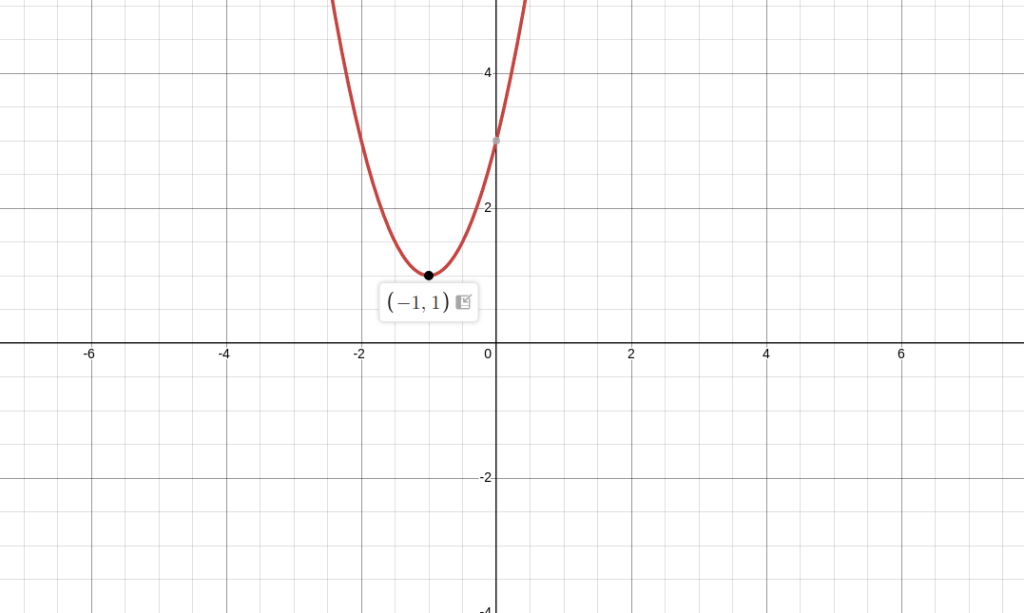
路人甲 :好神奇啊……这个函数的 开口向上,所以它有一个 y 能取到最小的最低点(顶点),这个坐标是……(-1,1)?
是啊,我们根据上节课的内容可以知道,当 常数项(c)增大时,相当于把每个点都向上移动了几个单位长度,所以说,在 y=2(x+1)2+1 里,常数项又成 1 了?是的!但是这个后面的 1 表示的是 顶点的 y 坐标,那x+ 1 中的 1 是顶点 x 坐标的相反数!
路人甲:所以究竟发生了什么啊!
其实非常简单,我们来理一下 顶点 的概念 , 顶点 的意思可以简单地理解为 y 取到最值的点(最大最小均可),在一个形如y=a(x+m)2+k 的二次函数的表达式中,我们可以 非常简单地得知顶点的坐标。以下是具体方法。
顶点公式的推演
众嗦周知,(x+m)2一定大于等于 0 ,当 a 为正数时, y 等于 k 加上一个大于等于 0 的数,这就很显然了, 当(x+m)2= 0 时,y 取到最值 。同理: a 为负数时, 当(x+m)2= 0 时,y 取到最值 。所以,当x+m=0 –> x=-m 时, y 取到最值(最大或最小),此时的 y 就等于 k !
路人甲 :哦……那么这时的 顶点坐标就是 (-m, k) 喽?
是哒!还记得我们一开始玩的那个东西吗?让我们回归 一般式的本质 ,看看:y=a(x+b/2a)2+(4ac-b2)/4a 的二次函数表达式就意味着此时:m=b/2a,k=(4ac-b2)/4a。很好啊!这顶点就很显然了。(b/2a, (4ac-b2)/4a)。
路人甲 :这不是……汪老师念叨的 顶点公式 吗?
是的,这个公式的妙处就在于可以让我们在 不去对一个相当复杂的二次函数表达式配方而得到顶点坐标 ,适当使用就有了 事半功倍 的效果!
路人甲 :等等……你这句话的意思是……有可能会 事倍功半?
事实……是这样的。当题目 接下来的步骤仍然需要顶点式 时,我还是建议 采用配方法 配出 顶点式。
一道例题
咳咳,来历练一下吧。
有一个二次函数表达式:ax2+2ax+4a (a≠0),请问:下列选项正确的是?
A、顶点位于第一或第三象限
B、顶点位于第二或第四象限
C、顶点位于原点
D、以上选项都是错误的
解:先求 顶点坐标 :发现这道题 very easy! 直接上!公!式!顶点坐标:(b/2a, (4ac-b2)/4a),此时a=a,b=2a,c=4a,直接计算得:(1, 0),在 x 轴上,所以选 D!
此次,我们用了 正解 ,也就是 顺着解题。
“When you look into an abyss, the abyss looks into you”
“当你凝视深渊的时候, 深渊也在凝视你”
番外
路人甲:你写这些不累吗?
麓黎:累啊,但是我有拖延症啊。要克服拖延症,就必须严于律己!
路人甲:你手里的书是啥?《如何远离拖延症》?
麓黎:嗯,这可是我新买的,看了它,一定能治好我的拖延症。
路人甲:哦?(翻开)
“第一章”
“我待会儿再写。“
麓黎 & 路人甲:(保持缄默)





